Βρίσκεστε εδώ: Αρχική Σελίδα >> Ιστορία του Φωτός >> Ειδική Θεωρία Σχετικότητας >> Χωρόχρονος
Μοιάζει παλαιομοδίτικη και ξεπερασμένη πια η άποψη του παγκόσμιου χρόνου, αλλά αξίζει να τη δούμε συνοπτικά (και σε ελεύθερη μετάφραση), όπως την περιέγραψε ο ίδιος ο Newton.
"Απόλυτα, η αλήθεια και ο χρόνος των μαθηματικών, κυλάνε μαζί, ανεξάρτητα από κάθε εξωτερική πηγή και λέγονται διάρκεια. Ο χρόνος όπως έχουμε συνηθίσει να το χρησιμοποιούμε στην καθημερινή μας ζωή, είναι μία λογική κι εξωτερική μέτρηση της διάρκειας. Η μέτρηση αυτή γίνεται με της κίνησης, αυτής τη διάρκεια μετράμε. Βέβαια αυτό που ονομάζουμε διάρκεια μιας μέρας, ενός μήνα ή ενός χρόνου δεν είναι ένας αντικειμενικός τρόπος μέτρησης του χρόνου, όμως αυτό συμβαίνει γιατί δεν υπάρχει μία εξίσωση που να μπορεί κανείς με τη βοήθειά της να μετρήσει με ακρίβεια το χρόνο. Όλες οι κινήσεις μπορούν να επιταχυνθούν ή να επιβραδυνθούν, αλλά η ροή του απόλυτου χρόνου δεν υπόκειται σε καμία αλλαγή".
Τι λένε τα παραπάνω λόγια; Ότι ένα γεγονός που συνέβη σε κάποιο χώρο, κάποια δεδομένη στιγμή έχει συμβεί στον ίδιο χρόνο και σε οποιοδήποτε άλλο μέρος. Συνεπώς οι μεταβολές, τα γεγονότα διαδίδονται με άπειρη ταχύτητα σε οποιοδήποτε σημείο του χώρου.
Στο σύμπαν του Galileo είχαν προταθεί διάφορα μέσα, μέσω των οποίων θα ταξίδευε το φως. Αυτό που είχε επικρατήσει, όπως αναφέρεται και σ' άλλο κεφάλαιο , ήταν ο αιθέρας, ένα υλικό, περίεργο, που δεν έμοιαζε ούτε με υγρό ούτε με αέριο, αλλά ήταν απλώς κάτι άλλο. Βέβαια σήμερα όλα αυτά έχουν καταρριφθεί. Το φως δε χρειάζεται κανένα μέσο για να διαδοθεί.
Εξαιτίας των επαναστατικών για την επιστήμη ανακαλύψεων του Einstein, ο Minkowski, κινήθηκε σε ένα πλαίσιο πολύ πιο ελεύθερο και τελικά πολύ πιο αποτελεσματικό. Θεώρησε λοιπόν, ότι δεν υπάρχει απόλυτος χρόνος, κάτι εξαιρετικά σημαντικό.
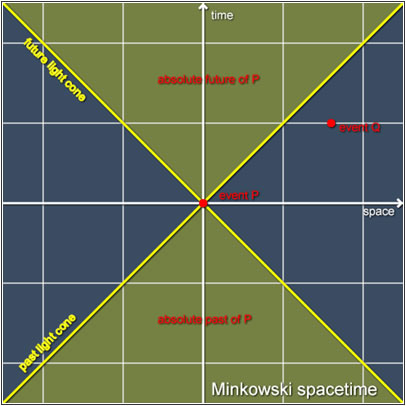Ο Minkowski χρησιμοποίησε ένα γεωμετρικό χώρο, κάθε μέρος του οποίου αντιπροσωπεύει ένα γεγονός. Αυτός ο χώρος γεγονότων ονομάζεται χωρόχρονος του Minkowski.
Χωρίς να μπούμε σε λεπτομέρειες, που θα μας αποπροσανατολίσουν ας δούμε τα βασικά χαρακτηριστικά του διαγράμματος του χωρόχρονου του Minkowski. Οι δύο ευθείες που περνάνε απ' την αρχή των αξόνων είναι οι διχοτόμοι των αντίστοιχων γωνιών και παίζουν σημαντικό ρόλο, αλλά δεν είναι καθόλου του παρόντος το να εξετάσουμε πως προήλθαν. Αν υποθέσουμε ότι στην αρχή των αξόνων συμβαίνει ένα γεγονός, τότε καθετί πάνω απ' τον άξονα χ ανήκει στο μέλλον του γεγονότος. Λογικό, αφού t>0. Αντίστοιχα, καθετί κάτω απ' τον άξονα αυτό, θ' ανήκει στο παρελθόν του γεγονότος. Βέβαια, όπως είδαμε και πριν στο παράδειγμα με τα βαγόνια, αυτό που λέμε χρονολογική τάξη γεγονότων δεν είναι κάτι απόλυτο. Με την εκλογή κάποιου άλλου συστήματος αναφοράς (ακόμα καλύτερα να το λέμε αδρανειακό σύστημα), το τι είναι παρόν παρελθόν και μάλλον μπορεί ν' αλλάξει. Ας μην παρασυρθούμε όμως σε αυτό το παιχνίδι.
Όμως κάτι, ένα γεγονός, είναι δυνατό να συμβεί όχι μόνο στην αρχή των αξόνων, αλλά και σε κάποιο άλλο σημείο του χώρου και του χρόνο (εξάλλου, αυτό ακριβώς προσπαθούμε τόση ώρα να δούμε πως γίνεται). Όταν, λοιπόν, συμβεί κάτι μέσα στην πράσινη περιοχή, τότε λέμε ότι αυτό το γεγονός είναι χρονοειδές. Αν ένα γεγονός συμβεί στην μπλε περιοχή λέγεται χωροειδές κι αν συμβεί πάνω σε οποιαδήποτε απ' τις δύο κίτρινες ευθείες, λέγεται φωτοειδές. Τα περίεργα αυτά ονόματα μάλλον δεν είναι και πολύ εποπτικά στο να κατανοήσουμε τι ήθελε ο Minkowski να πει, όμως χρειάζονται, όπως θα φανεί πιο κάτω.
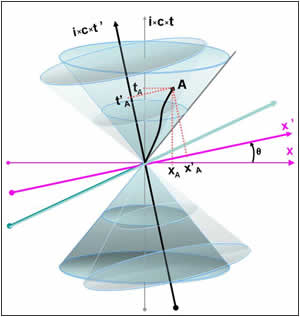Είναι χαρακτηριστικό ότι δεν έχουμε καθόλου μιλήσει για διάρκεια στο παρόν. Μάλλον είναι αυτονόητο, αν και στην καθημερινή μας ζωή δίνουμε διάρκεια στο παρόν. Στην πραγματικότητα όμως το παρόν είναι κάθε στιγμή, που μιλάμε ή σκεφτόμαστε αυτό, παρελθόν.
Τέλος, το παρακάτω σχήμα έρχεται για να ξεκαθαρίσει αυτό που λέμε ότι για ένα αδρανειακό σύστημα κάποιο γεγονός να ανήκει στο μέλλον, του τώρα, του παρόντος, αλλά για κάποιο άλλο αδρανειακό σύστημα, το ίδιο γεγονός μπορεί ν' ανήκει στο παρελθόν. Και στα δύο συστήματα το «τώρα» μας είναι το γεγονός Γ0, ενώ το Γ είναι ένα άλλο γεγονός. Στο αδρανειακό σύστημα με άξονες (χ,ct) το γεγονός Γ ανήκει στο μέλλον, ενώ για το σύστημα (χ',ct'), το οποίο φυσικά δεν είναι απαραίτητο να έχει τους άξονες κάθετους μεταξύ τους, ανήκει στο παρελθόν.
Το θέμα είναι ότι οι δύο ευθείες, πάνω στις οποίες «πατάνε» τα φωτοειδή γεγονότα, ορίζουν δύο κώνους τους κώνους φωτός, όπως λέγονται. Είναι ο κώνος του μέλλοντος κι ο κώνος του παρελθόντος, όπως φαίνονται και στο παρακάτω σχήμα. Εμείς δεν μπορούμε να επέμβουμε σ' αυτήν την περιοχή του "παγκόσμιου αλλού" ούτε να επηρεαστούμε απ' αυτή. Θα μπορούσε η περιοχή αυτή να είναι ένα άλλο σύμπαν, ας το πούμε έτσι. Προς το παρόν ας αρκεστούμε να λέμε ότι πρόκειται για κάτι που δεν μπορούμε να φανταστούμε τι είναι.
Μήπως μπορούμε τουλάχιστον να «παίξουμε» μέσα στους κώνους φωτός και να επηρεάσουμε τα γεγονότα; Ναι, θα ήταν πολύ εύκολο, αν υπήρχε η περίφημη χρονομηχανή, για την οποία πολλά έχουν κατά καιρούς ακουστεί. Τελικά, αυτό που έχουμε στα χέρια μας είναι μία αρκετά εποπτική προσομοίωση ενός κόσμου, που είμαστε μέλη, αλλά και κάποιων άλλων ίσως, για τους οποίους μάλλον δεν ξέρουμε τίποτα. Όλα αυτά κατά τον Minkowski, του οποίου πάντως το έργο είναι καθολικά αποδεκτό μέχρι σήμερα.
Σχετικοί Σύνδεσμοι (εξωτερικές σελίδες)