Βρίσκεστε εδώ: Αρχική Σελίδα >> Ιστορία του Φωτός >> Ο Αιθέρας >> Η προσομοίωση του πειράματος
Αφού ο Michelson είχε καταφέρει να μετρήσει με τόσο μεγάλη ακρίβεια την ταχύτητα του φωτός, η επόμενη πρόκληση που είχε στο μυαλό του ήταν η μελέτη του αιθέρα. Φυσικά, κάτι που υπάρχει παντού και την ίδια στιγμή επιτρέπει στα υλικά σώματα να κινούνται ελεύθερα, είναι πολύ δύσκολο να ανιχνευθεί και να μελετηθεί.
Ο Michelson τότε είχε μια πολύ καλή και ξεκάθαρη ιδέα για να μετρήσει τον άνεμο του αιθέρα. Όπως εξήγησε στα παιδιά του (με βάση τα λόγια της κόρης του) το θέμα βασιζόταν στον εξής γρίφο: "Ας υποθέσουμε ότι έχουμε ένα ποταμό με πλάτος 100 μέτρα, δύο κολυμβητές, που μπορούσαν να κολυμπήσουν με μια ταχύτητα 5 μέτρων το δευτερόλεπτο και ότι το νερό ρέει με μια ταχύτητα 3 μέτρων το δευτερόλεπτο. Οι δύο κολυμβητές αρχίζουν έναν αγώνα ταχύτητας με τους εξής κανόνες: Και οι δύο ξεκινάνε απ' την ίδια πλευρά του ποταμού. Ο πρώτος θα πρέπει να φτάσει στο ακριβώς πλησιέστερο σημείο της απέναντι όχθης του ποταμού και να επιστρέψει στο σημείο εκκίνησης. Ο δεύτερος πρέπει να κολυμπήσει κόντρα στο ρεύμα του ποταμού για μία απόσταση όσο το πλάτος του ποταμού (δηλαδή 100 μέτρα) και μετά να επιστρέψει στο σημείο εκκίνησης. Ποιος θα νικήσει;"
Ας δούμε πρώτα το χρόνο του δεύτερου κολυμβητή. Ο χρόνος που του χρειάζεται για να διανύσει απόσταση όσο το πλάτος του ποταμού, δηλ. 100 μέτρα, είναι 50 δευτερόλεπτα, αφού η σχετική του ταχύτητα είναι 2 μέτρα το δευτερόλεπτο. Για την επιστροφή στο σημείο εκκίνησης θα χρειαστεί μόνο 12,5 δευτερόλεπτα, εφόσον η ταχύτητά του θα είναι τώρα 8 μέτρα ανά δευτερόλεπτο. Συνολικά θα κάνει 62,5 δευτερόλεπτα, λοιπόν.
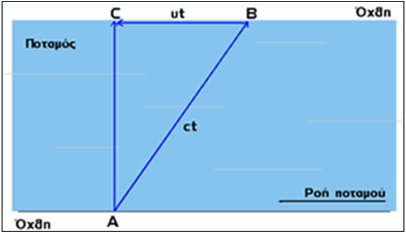
Το σχήμα είναι κατατοπιστικό όσον αφορά την πορεία του πρώτου κολυμβητή. Αν ονομάσουμε c την ταχύτητα του και u την ταχύτητα του νερού του ποταμού, τότε βλέπουμε τα εξής. Ο πρώτος κολυμβητής είναι πιο πονηρός. Δεν κολυμπά έχοντας πορεία ακριβώς προς την απέναντι όχθη, επειδή γνωρίζει ότι το νερό θα τον παρασύρει κατά κάποια απόσταση. Οπότε κολυμπά με κάποια κλίση, υπολογισμένη από πριν (αν και στην πραγματικότητα αυτή η διαδικασία γίνεται αυτόματα φυσικά), με σκοπό να φτάσει στο ακριβώς απέναντι σημείο απ' αυτό της εκκίνησης, στο σχήμα είναι το σημείο Β. Έτσι ο πρώτος κολυμβητής κολυμπά με μια ταχύτητα 5 μέτρων ανά δευτερόλεπτο, υπό κάποια γωνία και ταυτόχρονα μεταφέρεται από το νερό του ποταμού, κατά τη διεύθυνση της ροής του με μια ταχύτητα 3 μέτρων το δευτερόλεπτο. Με δεδομένο πάντα ότι οι υπολογισμοί του κολυμβητή αυτού, όσον αφορά το τόξο, είναι ακριβείς, τότε μπορούμε να πούμε ότι σε ένα δευτερόλεπτο έχει διανύσει απόσταση τεσσάρων μέτρων κάθετα στις όχθες του ποταμού. Το συμπέρασμα αυτό προκύπτει εύκολα εφαρμόζοντας το πυθαγόρειο θεώρημα στο τρίγωνο που σχηματίζεται στο σχήμα.
Έτσι χρειάζεται 25 δευτερόλεπτα για να φτάσει στην απέναντι όχθη του ποταμού και προφανώς θα χρειαστεί άλλα 25 για να επιστρέψει. Συνολικά θα χρειαστεί 50 δευτερόλεπτα και συνεπώς θα είναι ο νικητής.
Σχετικοί Σύνδεσμοι (εξωτερικές σελίδες)