Βρίσκεστε εδώ: Αρχική Σελίδα >> Ιστορία του Φωτός >> Το πείραμα των δύο σχισμών >> Φως ως σωματίδιο
Ας μπούμε στην "καρδιά" του πειράματος.Υποθέτουμε, όπως φαίνεται και στο παρακάτω σχήμα ότι έχουμε ένα όπλο και σε κάποια απόσταση από αυτό ένα θωρακισμένο διάφραγμα με μια τρύπα, μέσα απ' την οποία μπορούν να διέρχονται τα βλήματα. Σε αρκετή απόσταση από το διάφραγμα με την τρύπα υπάρχει ένα άλλο, εντελώς όμοιο με το πρώτο, μόνο που αντί για μία τρύπα έχει δύο. Για χάρη ευκολίας ονομάζουμε τις δύο αυτές τρύπες, τρύπα Νο 1 και Νο 2. Οι τρύπες επιτρέπουν τη διέλευση των βλημάτων, των σφαιρών που εκπυρσοκροτεί το όπλο. Πιο πέρα από το δεύτερο διάφραγμα υπάρχει ένας ανιχνευτής, οποίος μπορεί να κινείται κατακόρυφα. Η δουλειά αυτού του ανιχνευτή είναι να μετρά τον αριθμό των σφαιρών που πέφτουν σε διάφορα σημεία πίσω απ΄ το δεύτερο διάφραγμα στη μονάδα του χρόνού. Το χ δεν είναι τίποτ' άλλο από την απόσταση του ανιχνευτή από κάποιο σταθερό σημείο (βλ. σχήμα).
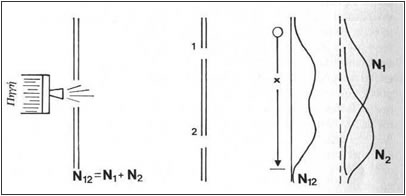Αυτό που έχουμε να κάνουμε τώρα εμείς είναι να μετράμε τον αριθμό των βλημάτων, των σφαιρών που φτάνουν σε κάποιο ή μάλλον σε όλα τα σημεία του χώρου πίσω από το δεύτερο διάφραγμα. Ας υποθέσουμε για ευκολία ότι μετράμε για μία ώρα και μετά βλέπουμε πόσα βλήματα έχουν φτάσει στα σημεία πίσω από το δεύτερο διάφραγμα. Τον αριθμό αυτόν, των βλημάτων μπορούμε να τον ονομάσουμε πιθανότητα άφιξης ενός βλήματος στην περιοχή χ, επειδή μας δίνει κάτι ανάλογο προς την πιθανότητα άφιξης του βλήματος. Αυτό που προκύπτει μετά το πέρασμα κάποιου χρονικού διαστήματος, της μίας ώρας όπως υποθέσαμε πριν είναι μια καμπύλη, όπως αυτή που φαίνεται στο πιο πάνω σχήμα και που την ονομάζουμε καμπύλη Ν12. Η καμπύλη αυτή δείχνει ότι περισσότερα βλήματα φτάνουν στο χώρο που βρίσκεται ακριβώς πίσω από τις δύο τρύπες κι όσο απομακρυνόμαστε από αυτές όλο και λιγότερα φτάνουν.
Είναι αυτό που λέγαμε πριν. Είναι φυσικά αδύνατο να σκεφτεί κάποιος ότι τα βλήματα ενός όπλου θα περάσουν την πρώτη σχισμή και μετά με κάποιο τρόπο θα στρίψουν και θα περάσουν πίσω από τις δύο σχισμές. Αν όμως δεν είμαστε πιο ελαστικοί στον τρόπο που σκεφτόμαστε, είναι πολύ δύσκολο να καταλήξουμε εκεί που θέλουμε. Όμως το παράδοξο είναι ότι, (αφού δεχθούμε το γεγονός ότι τα βλήματα μπορούν να παρεκκλίνουν της ευθύγραμμης πορείας τους), μας φαίνεται αρκετά φυσιολογικό το ότι παίρνουμε μια καμπύλη της μορφής Ν12 για τις θέσεις πίσω από τις δύο σχισμές. Η μορφή αυτή, εξάλλου υποδηλώνει τον τρόπο που περνούν τα βλήματα από τις τρύπες Νο 1 και Νο 2. Ακόμα πρέπει να πούμε ότι ο αριθμός των βλημάτων που φτάνουν σε κάποια θέση σε κάποια άλλη μονάδα του χρόνου δεν είναι απαραίτητο να είναι ακέραιος, χωρίς όμως να ξεχνάμε ότι τα βλήματα είναι μικρές ατσάλινες σφαίρες και δεν μπορούν να σπάσουν.
Τι είναι όμως η Καμπύλη Ν12; Άνετα θα μπορούσε να είναι το άθροισμα που προκύπτει απ' την πρόσθεση των δύο άλλων καμπύλων, ας πούμε των καμπύλων Ν1 και Ν2 οι οποίες προκύπτουν ως εξής. Η Καμπύλη Ν1 δείχνει τον αριθμό των βλημάτων που φτάνουν πίσω από την τρύπα Νο1, όταν εμείς έχουμε κλείσει την τρύπα Νο2 με ένα θωρακισμένο κάλυμμα. Τελείως αντίστοιχα προκύπτει και η καμπύλη Νο2. Καταλήγουμε, με αυτή τη λογική σε ένα σημαντικό νόμο: Ο αριθμός των βλημάτων που διέρχονται κι από τις δύο σχισμές είναι το άθροισμα του αριθμού των βλημάτων που διέρχονται από τη σχισμή Νο1 κι από τη σχισμή Νο2. Ας ονομάσουμε όλη αυτή τη διαδικασία της πρόσθεσης των αριθμών των βλημάτων "σύνθεση χωρίς συμβολή". Δηλαδή:
N12=N1+N2, (χωρίς συμβολή)