You are here: Home >> Encyclopedia of Light >> Wavelength
According to the modern theory concerning atoms, electrons move in orbits around the nucleus.If an electron absorbs energy it is promoted to a higher energy orbit.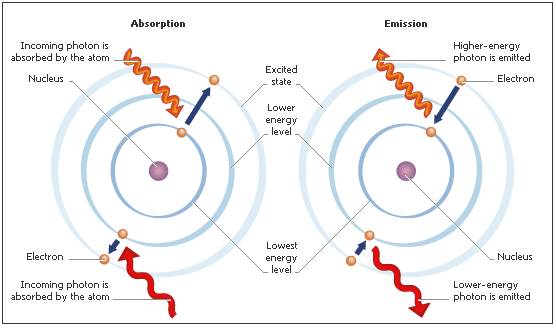 
This situation is so unstable that after a very small period of time (much less than a second) and then it falls back to its previous orbit. During the fall it emits a photon. The energy of a photon depends on radiation frequency; there are photons of all energies from high-energy gamma- and X-rays, through visible light, to low-energy infrared and radio waves. All photons travel at the speed of light. Photons do not have electric charge or rest mass and one unit of spin; they are field particles that are thought to be the carriers of the electromagnetic field.
The wavelength of light λ (in meters), is related to the frequency v (in HZ) and to the speed of light c, by the equation:
λ = c/v
where c is the speed of light with a constant value of 300 million meters per second, is the frequency of the light in hertz (Hz) or cycles per second, and is the wavelength of the light in meters. From this relationship it is clear that the wavelength of light in inversely proportional to the frequency. An increase in frequency produces a proportional decrease in the wavelength of light with a corresponding increase in the energy of the photons that make up the light. Upon entering a new medium (such as glass or water), the speed and wavelength of light is reduced, although the frequency remains unaltered.
Explore how an electron absorbs energy, is excited into a higher energy state, and then decays at the Laboratory of Light
The relationship between the energy of a photon and it's frequency is dictated by another simple equation:
E = hv = hc/λ
where E is the energy in kiloJoules per mole, h is Planck's constant with a value of 6.626 x 10-34 Joule-seconds per particle, and the other variables were defined above.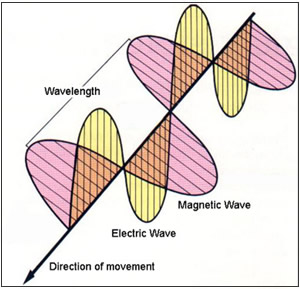 
From this equation, it is clear that the energy of a photon is directly proportional to its frequency and inversely proportional to its wavelength. Thus as frequency increases (with a corresponding decrease in wavelength), the photon energy increases and visa versa.
Next figure illustrates the propagation of an electromagnetic wave in a direction from upper left to lower right. This wave travels at the speed of light and is known as a transverse wave where the direction of wave energy lies at right angles to the direction of propagation.
In this example, the wave is generating both electric and magnetic oscillating fields that are oriented at 90 degree angles with respect to each other and also to the direction of energy. The distance between two successive peaks in the illustration equals the wavelength of the radiation. The number of oscillations (equal to a single sinusoidal) per second equals the frequency of the radiation, which is usually measured in hertz (cycles per second).