You are here: Home >> Encyclopedia of Light >> Refraction
What follows reflection is refraction. The two phenomena are certainly different, but there is a relation between them. When light is considered to be a wave and passes from one transparent medium to another it changes its direction, because its velocity is different in two mediums. This description concerns refraction. We know that in space light has a velocity of c=300.000.000 km/s. When light crosses a transparent medium it changes its velocity to a lower but certain one.
Refractive index n, is a new concept which represents the amount of refraction and it is equal to the velocity c of light of a given wavelength in empty space divided by its velocity v in a substance, or
n = c / v
If i is the angle of incidence of a ray in vacuum (angle between the incoming ray and the perpendicular to the surface of a medium, called the normal), and r is the angle of refraction (angle between the ray in the medium and the normal), the refractive index n is also defined as the ratio of the sine of the angle of incidence to the sine of the angle of refraction;
n = sin i / sin r
This is a second way to define refractive index.
In 1621 a the Dutch astronomer and mathematician Willebrord van Roijen Snell proposed a mathematical equation which describes refraction. The account of Snell's law went unpublished until its mention by Christiaan Huygens in his treatise on light.
In 1621 a the Dutch astronomer and mathematician Willebrord van Roijen Snell proposed a mathematical equation which describes refraction. The account of Snell's law went unpublished until its mention by Christiaan Huygens in his treatise on light.
If n1 and n2 represent the indices of refraction for two media, and α1 and α2 are the angles of incidence and refraction Snell's law asserts that
n1 * sin(α1) = n2 * sin(θ2)
The index of refraction varies inversely with the speed of a wave of light in a transparent medium. Any transparent medium-e.g., a glass prism-will cause an incident parallel beam of light to fan out according to the refractive index of the glass for each of the component wavelengths, or colours.
Refraction is responsible for many strange to our eyes phenomena. A common example is a straw inside a glass of water. The part of the straw which lies inside the pencil appears to be bent and magnified. To explain this paradox we have to think that the waves of light have a different velocity in water, glass and air and as a result they are shifted to different degrees among the mediums.
Refraction and reflection are relational phenomena when we examine the critical angle of refraction. What does it mean? Given that a ray is bent away from the normal when it enters a less dense medium and that the deviation from the normal increases as the angle of incidence increases, an angle of incidence exists such that the refracted ray makes an angle of 90° with the normal to the surface and travels along the boundary between the two media. If the angle of incidence is increased beyond the critical angle, the light rays will be totally reflected back into the incident medium. Total reflection cannot occur if light is traveling from a less dense medium to a denser one.
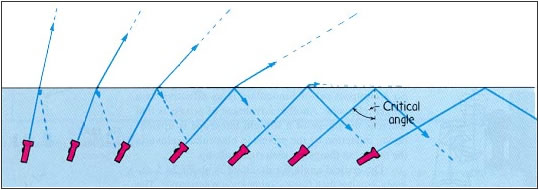
The phenomenon of Total Reflection at the Laboratory of Light
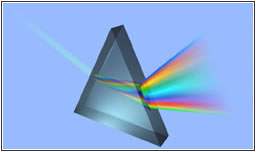Let us see what happens in a prism. Prisms can separate white light into its constituent colours, called a spectrum. Each colour, or wavelength, making up the white light is refracted, a different amount; the shorter wavelengths (those toward the violet end of the spectrum) are bent the most, and the longer wavelengths (those toward the red end of the spectrum) are bent the least. Prisms of this kind are used in certain spectroscopes, instruments for analyzing light and for determining the identity and structure of materials that emit or absorb light.
How prisms work at the Laboratory of Light