Βρίσκεστε εδώ: Αρχική Σελίδα >> Θεωρία Γραφημάτων >> H ιστορία της Θεωρίας Γραφημάτων
Ο W. Leibniz σε επιστολή του το 1679 προς τον C. Huygens παρατήρησε ότι"μας χρειάζεται ένα άλλο είδος ανάλυσης γεωμετρικής ή γραμμικής, που να ασχολείται απευθείας με τη θέση, όπως η Άλγεβρα ασχολείται με το μέγεθος". Μάλιστα, χρησιμοποίησε τον όρο "analysis situs" δηλ. ανάλυση της θέσης για το είδος αυτό της ανάλυσης, το οποίο κατά καιρούς ονομάστηκε "geometria situs" ή "geometry of position" για να καταλήξει σήμερα στον όρο Θεωρία Γραφημάτων.
Η Θεωρία Γραφημάτων λοιπόν, ασχολείται με την απεικόνιση πολύπλοκων ή μη προβλημάτων μέσω της αναπαράστασής τους σε σχήματα.
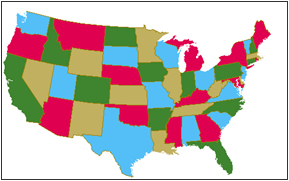
Το πρόβλημα πρωτοδιατυπώθηκε από τον Mobious το 1840 κι αφορά στη δυνατότητα χρωματισμού οποιουδήποτε χάρτη με τέσσερα μόνο χρώματα. Το σκεπτικό ήταν αντί να γίνουν διάφοροι μαθηματικοί υπολογισμοί, να γίνει μια προσπάθεια απεικόνισης του προβλήματος και μέσω της απεικόνισης αυτής να λυθεί το πρόβλημα. Είναι χαρακτηριστικό ότι μόλις το 1976 και με τη βοήθεια ηλεκτρονικού υπολογιστή και πολύπλοκων μαθηματικών υπολογισμών επιβεβαιώθηκε ότι πράγματι, τέσσερα χρώματα αρκούν για το χρωματισμό κάθε χάρτη.
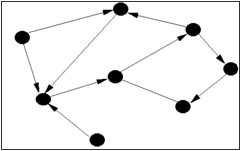Σημεία και τόξαΧρησιμοποιώντας όρους της Θεωρίας Γραφημάτων σε γενικές γραμμές κάθε γράφημα αποτελείται από μια διαδοχή από Σημεία (nodes) και Τόξα (arcs). Τα τόξα μπορούν να έχουν μια συγκεκριμένη κατεύθυνση ή όχι ανάλογα με το πρόβλημα που αντιμετωπίζεται.
Για να γίνει πιο κατανοητή η Θεωρία Γραφημάτων παρουσιάζεται το παρακάτω πρόβλημα: Επιδιώκεται σύνδεση τεσσάρων δεξαμενών που δεν έχουν πρόσβαση σε νερό (Δεξαμενές 1-4) με μία (Δεξαμενή 5) η οποία έχει πρόσβαση σε νερό. Οι δεξαμενές πρέπει να ενωθούν με ένα σωλήνα, οποίος θα διέρχεται από όλες. Το σχήμα που ακολουθεί παρουσιάζει τις δεξαμενές αυτές, καθώς και το κόστος που απαιτείται για κάθε μία επιμέρους σύνδεση.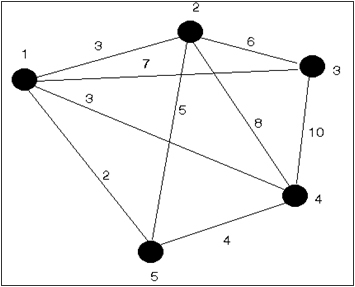 
Για το λόγο ότι επιθυμείται το μικρότερο δυνατό κόστος η διαδρομή π.χ. 1-2-3-4-5-1 είναι πιο συμφέρουσα [καθώς έχει συνολικό κόστος (3+6+10+4+2)=25] από τη διαδρομή π.χ. 1-5-4-2-3-1 [που έχει συνολικό κόστος (2+4+8+6+7)=27].
Είναι φανερό ότι το παραπάνω πρόβλημα μπορεί να θεωρηθεί ότι καλύπτει μια σειρά αναλόγων προβλημάτων. Η προσπάθεια λύσης αυτών με αυστηρά μαθηματικές μεθόδους είναι σαφώς πιο δαπανηρή σε σκέψη και προσφέρει λιγότερη εποπτικότητα από αυτή που επιτυγχάνεται με τη βοήθεια της Θεωρίας Γραφημάτων.
Ένα χαρακτηριστικό της Θεωρίας Γραφημάτων είναι το γεγονός ότι πρόκειται για μία θεωρία, η οποία μπορεί να μεταβληθεί ανάλογα με το πρόβλημα που αντιμετωπίζεται κάθε φορά. Πρόκειται δηλαδή για μία "εύκαμπτη" προσέγγιση του εκάστοτε προβλήματος. Αν και υπάρχουν αρκετές προσπάθειες ομαδοποίησης προβλημάτων ώστε να μπορούν να εξετασθούν πιο εύκολα, οι ανάγκες της συγκεκριμένης μελέτης γύρω από τη φύση του φωτός μας περιορίζουν στην συγκεκριμένη προσέγγιση που θα παρουσιασθεί στις επόμενες ενότητες.